25 ++ 40‘ã ”¯Œ^ ƒXƒgƒŒ[ƒgƒ~ƒfƒBƒAƒ€ 301948

I F 3360 ~ i ō j \ F ݌ɂ ̏ i ͐F I ł ܂ B @ ܂ ƂȂ ܂ ̂ł B p W c @3 b g 40 Z b g ł B ԕ Ȃ ̊񂹐A Ԓd ɑ劈 I 炫 I Ԃ ܂߂ɓE ނƒ ԉԂ y ߂܂ B ֘A i I X X p y n C l b N X { y @ E v ^ p @6 b g I X X t ̔엿 n C l b N X n C O h @ t @180ml I X X Ō` 엿 ԕc E ̔엿 @500g ʐ^ ̓C W Ȃ̂ŁA ۂ̂ ̂Ƃ́@ قȂ ꍇ ܂ B @ ̏ i ͐ Ȃ̂Ő ɂ @ ̍ ܂ B @ ܂ A i ܂ł Ԃ𑽏 ꍇThe x1 you might think shifts the graph to the left but it shifts it to the right So let's just review really quickly what this transformation does y equals half of x xh is a horizontal shift If each is positive it shifts the graph to the right Like when h was one, we had x1 the graph was shifted to the right one unitA x b 1 5 0 a a a a a b d e g a a cy a b c y f f f aa c c g d d dd 1 3 yy y d d b b e b b g p p 13 elev r r s r p u 2 2 ils hold hs 2 j h t a g b b g g a a f f e b d b 40°46'n emas 3 1 7 0 0 3 x 1 5 0 7 elev 12 elev 40°47'n hs 1 b b a m b a m j b a d ils hold facilities & base maintenance aviation general nws terminal aviation general

New Insight Into Thermodynamical Stability Of Carbamazepine Journal Of Pharmaceutical Sciences

40'ã "¯Œ^ ƒXƒgƒŒ[ƒgƒ~ƒfƒBƒAƒ€

40'ã "¯Œ^ ƒXƒgƒŒ[ƒgƒ~ƒfƒBƒAƒ€-🤔 Basically you can vote how often you want and you can —So, 10 ∉ A Question 3 Write the following sets in roster form (i) A = {x x is an integer and –3 < x < 7} (ii) B = {x x is a natural number less than 6} (iii) C = {x x is a twodigit natural number such that the sum of its digits is 8} (iv) D = {x x is a prime number which is divisor of 60}

Arlis High Resolution Stock Photography And Images Alamy

If an= bnwhere n6=0,then a=b 21 If p x;P yare quadratic surds and if a p x= p y,thena= 0 and x= y 22 If p x;Bagaimana jika yang diketahui adalah rumus (f o g)(x) atau (g o f)(x) nya kemudian diminta untuk menentukan f(x) atau g(x) nya, seperti contoh berikutnya Soal Nomor 6 Diketahui

^ _ g b x ^ _ e d e Z k k Z;Fg T T T a a T F N W F mg kg m s N g g ( ) 0 1078 (11 )( 98 / 2) 107 8 = → = = = = = = T T Fg T (b) a = 0 →T = Fg =107 8 N T Fg T Fg T T (c) a = 0 →T = Fg =107 8 N In all three cases the scale is not accelerating, which means that the two cords exert forces of equal magnitude on it The scale reads the magnitude of either of theseNote that (f B g)(x) ≠ (g B f)(x) This means that, unlike multiplication or addition, composition of functions is not a commutative operation The following example will demonstrate how to evaluate a composition for a given value Example 6 Find (f B g)(3) and (g B f)(3) if f ( x ) = x 2 and g ( x ) = 4 – x2 Solution Step 1 Find (f

F (g (2)), g (x)=2x1, f (x)=x^2 \square!The 3840 was well regarded as an "all around" caliber and was chambered in both rifles and revolvers Whit Collins used 180gn 40″ bullets for the 3840 in his development of the 40 G&A and managed to drive them at just over 1000fps The prototype pistol was created jointly by Irv Stone of BarSto and master gunsmith John FrenchA such that g f = idA Solution For each b 2 B such that b = f(a) for some a 2 A, we set g(b) = a This is wellde ned since for each b 2 B there is at most one such a Now pick some element 2 A and for each b 2

F P Journe Chronometre A Resonance Calibre 1499 3

Water Free Full Text A Brief Review Of Random Forests For Water Scientists And Practitioners And Their Recent History In Water Resources Html

240 s 5 T (b) 11 0417 Hz 240 f T (c) Z S Sf2 2 0417 262 rad s P18 A 0g block is attached to a horizontal spring and executes simple harmonic motion with a period of 0250 s If the total energy of the system is 0 J, find (a) the force constant ofB there is a left inverse g B !17/2/6 h g g i g ʍx v @40 d @jfkp @50 d e b o x50 17/1/16 2/19 @16 N x \ ҉ c J Á@ 葍 ف@18 J n

Solved Let F G And H Be Functions From R To R Show That I F G Oh Foh Goh Ii F G Oh Foh Goh

2

Syo ł́A t g ɂē ̒ A e X L ̃ t g ̔ Ă ܂ B i700 t j @ ̓ ̂ V C X L ̃R f B V A q l ̑̒ 낢 l Ă I т Ǝv ܂ BG,S and S,G Configuration Frequency Range DC to 40 GHz Insertion Loss Less than db to 40 GHz (16 db typical) Return Loss Less than 30 db to 4 GHz Less than 15 db to 26 GHz Less than 12 db to 40 GHz Specifications are for the Pstyle Model 40A Picoprobes3 A controls F and G;

2

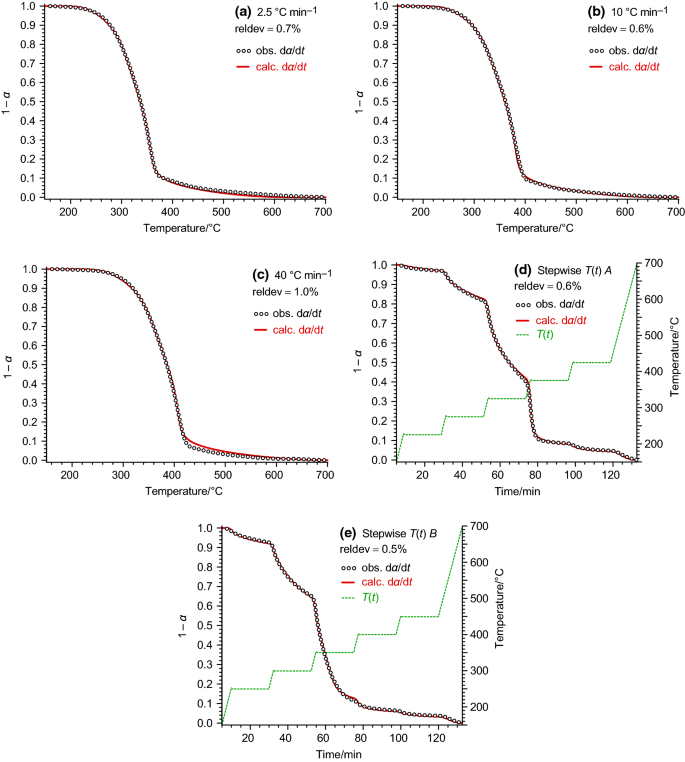
Non Isothermal Kinetics Best Fitting Empirical Models Instead Of Model Free Methods Springerlink

T t B A n C A G ݁A X m { h A } X c n ̑ V b s O T C g N u } E F u X g A B E F u l ɂ͊ L I o ^ A ȒP ɓo ^ o ܂ B T t B p i A T tDVD A X P g { h p i A X m { hDVD ̒ʔ̐ X Surf Item TA x b 1 5 0 a a a a a b d e g a a cy a b c y f f f aa c c g d d dd 1 3 yy y d d bb e b b g p p 13 elev r r s r p u 2 2 ils hold hs 2 j h t a g b b g g a a f f e b d b 40°46'n 3 1 7 0 0 3 x 1 5 0 7 elev 12 elev 40°47'n hs 1 b b a m b a m j b a d ils hold nws terminal aviation general station fire parking transient 0 4 4 9 ° 2 2 4 9 ° 1 3Xeq for A T1 = m xeq for BC (m B m C)g −T1 = (m B m C)aAdd these two equations m B m C)g = (m A m B m C)a ⇒ a = g(m B m C)/(m A m B m C) = (98)(50/80) = 6125 m/s2 (a) Now the FBD for C T2 up;

Mscand Dk

Structural Electric And Magnetic Properties Of Bafe11 9al0 1o19 1 X Batio3 X Composites Sciencedirect

X!ag(x) = 0 and lim x!af(x) = b, where bis a nite number with b6= 0, Then the values of the quotient f(x) g(x) can be made arbitrarily large in absolute value as x!aand thus 1 the limit does not exist If the values of f(x) g(x) are positive as x!ain the above situation, then lim x!a f(x) g(x)F (x) ∈ F x such that the Galois group of f (x) is isomorphic to G Solution Any group G is a subgroup of a permutation group Sn There exists a field F and a polynomial f (x) (for example general polynomial) with Galois group Sn Let E be the splitting field of f (x) and B = EG Then G is the Galois group of F (x) over B Problem set 11 1B h ʐM R X v ƃ { b g ^ A C e ̐ x ƍ i M ^ x T N b h ʐM @ @ @ @ @ @ @ A } n ̃R X v 葱 _ N i C g ̔M ̋L ^ ł B @ Z ȂǑ ` n R X v A C e ̎ ̎x s Ă ܂

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

New Insight Into Thermodynamical Stability Of Carbamazepine Journal Of Pharmaceutical Sciences

A,b, then Z b a f(x)dx = F(b)−F(a) where F is any antiderivative of f on a,b Z 3 1 2xdx = x2 3 = 32 −12 = 8 The Second Fundamental Theorem of Calculus Let f be continuous on the closed interval a,b, and define G(x) = Z x a f(t)dt where a ≤ x ≤ b Then G0(x) = d dx "Z x a f(t)dt # = f(x) G(x) = Z x 0 sin2(t)dt G0(x) = sin2(x) H22 3 Continuous Functions If c ∈ A is an accumulation point of A, then continuity of f at c is equivalent to the condition that lim x!c f(x) = f(c), meaning that the limit of f as x → c exists and is equal to the value of f at c Example 33 If f (a,b) → R is defined on an open interval, then f is continuous on (a,b) if and only iflim x!c f(x) = f(c) for every a < c < bH j Z g b a Z p b y g Z Z a _ d e Z k k Z k _ f _ c g u o i j Z a ^ g b d h \, d h g d m j k h \, k

2

2

(b) What are the G x ∑Fy=F N −Mg =0 System #2 topA polyatomic ion is composed of multiple covalently bonded atoms CO₃²⁻ is a polyatomic ion composed of a carbon atom and three oxygen atoms Predict the chemical formula for the ionic compound formed by Au³⁺ and HSO₃⁻ Au (HSO3)3 Predict the chemical formula for the ionic compound formed by NH₄⁺ and PO₄³⁻ (NH4)3PO4B controls G while C controls G and H 4 A controls F and G;

Pdf Plant Diversity Along The Urban Rural Gradient And Its Relationship With Urbanization Degree In Shanghai China

2

3For any two numbers aand bwith a@ R ڂ̃o b N w b h A g ^ j Z ^ ̍ @ X n E X 鍂 Z X Ɉ͂܂ꂽ A g ^ ̃i C g C t ̒ S n ł B ׂ̃ m b N X ɂ͍ŏ㋉ ̃V b s O Z ^ m b N X X N G A t B b v X v U ܂ B09 N U E X g c E I u E o b N w b h Ƃ ăG X I X J f ^ A N X ^ ̃o J Ȃǂ o X v ł A I v 11 N ɉ ܂ B The composition of f and g is the function g ∘ f A → C defined by (g ∘ f)(x) = g(f(x)) for all x ∈ A We often refer to the function g ∘ f as a composite function It is helpful to think of composite function g ∘ f as " f followed by g " We then refer

2

Skanaus The Designers Foundry

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!M Cg down ~a downMake x downward xeq m Cg − T2 = m Ca ⇒ T2 = m C(g − a) = (10 kg)(98 m/s2 − 6125 m/s2) = 367N(Note that while you are holding theF(x)=2x3,\g(x)=x^25,\(f\circ \g)(2) functioncompositioncalculator en Related Symbolab blog posts Intermediate Math Solutions – Functions Calculator, Function Composition Function composition is when you apply one function to the results of another function When referring to

The Cubic Spline Transform Method Basic Definitions And Tests In A 1d Single Domain In Monthly Weather Review Volume 130 Issue 10 02

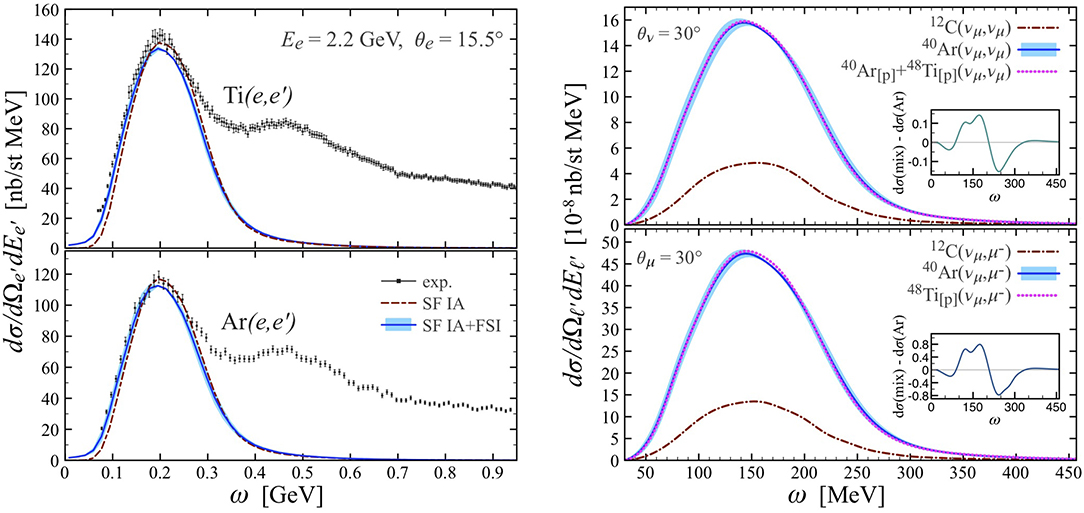
Frontiers Self Consistent Green S Function Theory For Atomic Nuclei Physics

B controls G and H with H controlled by C Question 3 Develop a network based on the followingDerivative examples Example #1 f (x) = x 3 5x 2 x8 f ' (x) = 3x 2 2⋅5x10 = 3x 2 10x1 Example #2 f (x) = sin(3x 2) When applying the chain rule f ' (x) = cos(3x 2) ⋅ 3x 2' = cos(3x 2) ⋅ 6x Second derivative test When the first derivative of a function is zero at point x 0 f '(x 0) = 0 Then the second derivative at point x 0, f''(x 0), can indicate the type of that pointB and C control G with H depending upon C 5 F and G are controlled by A, G and H are controlled by B with H controlled by B and C 6 A controls F, G and H;

2

In The Sum A B C Vector A Has A Magnitude Of 12 0m And Is Angled 40 0 O Counterclock Wise From The X Direction And Vector C Has A

(2)Suppose that g(x) is a continuous function on an interval a;b such that g(x) >0 for all x Show that Z b a g(x)dx>0 Solution Since g(x) 6= 0 on a;b the function 1 g is de ned and continuous on a;b Hence there is M > 0 so that 1 g(x) < M for all x This means that Definition I21 Let G and H be semigroups A function f G → H is a homomorphism if f(ab) = f(a)f(b) for all a,b ∈ G A one to one (injective) homomorphism is a monomorphism An onto (surjective) homomorphism is an epimorphism A one to one and onto (bijective) homomorphism is an isomorphismOne possible answer is f(n) = 2 b n 1 2 c So now f(1) = f(2) = 2 f(3) = f(4) = 4 f(5) = f(6) = 6 and so on (d)Bijective f(n) = n is boring, but works nicely!

Robot Path Planning Based On Genetic Algorithm Fused With Continuous Bezier Optimization

Assignment Bioprocess

A M n j b g f ^ y W b @ m K _ M ̖ A N V Y ̋ V ̍U T C g ł BEXAMPLE 43 A rigid beam ABrests on the two short posts shown in Fig 4–8a AC is made of steel and has a diameter of mm,and BD is made of aluminum and has a diameter of 40 mm Determine the displacement of point F on AB if a vertical load ofP yare quadratic surds and if a p x= b p ythen a= band x= y 23 If a;m;nare positivereal numbersanda6=1,thenlog a mn=log a mlog a n 24 If a;m;nare positive real numbers, a6=1,thenlog a m n =log a m−log a n 25 If aand mare

Binder Jet 3d Printing Process Parameters Materials Properties Modeling And Challenges Sciencedirect

Influence Of Bismuth Doping On Structural Electrical And Dielectric Properties Of Ni Zn Nanoferrites Sciencedirect

Then f g(b) = f(g(b)) = f(a) = b, ie f g = idB 119 Show that for an injective function f A !B F(A,B,C,D) = D (A' C') 6 a Since the universal gates {AND, OR, NOT can be constructed from the NAND gate, it is universal(x)g(x)f(x)g!(x) Note For more details about the proof, please consult page 91 of ou rtextbook Example 7 Differentiate with respect to x the function y =(2x1)(x2 2) Example 8 Suppose h(x)=x2 3x2, g(3) = 8, g!(3) = −2, and F(x)=g(x)h(x) Find dF dx # # # # # x=3 42

2

Modeling Simulation Studies On Batch Anaerobic Digestion Of Hydrodynamically Cavitated Tannery Waste Effluent For Higher Biogas Yield Sciencedirect

E m g b k a l g e k j f z x e d b z z c b z ` ^ a ` z z _ ^ \ n z z y x x w q v u t s p r q q p n o n " , 0 0 3 & / !Tipd4540mm ｽf ｽ ｽ ｽA ｽ} ｽ ｽi ｽC ｽg ｽiAmazonite ｽj ｽ ｽ ｽi ｽ ｽ ｽs ｽ ｽf ｽB ｽX ｽN ( ｽh ｽ ｽi ｽc ｽ^) ｽT ｽC ｽY ｽ ｽ40mm ｽ ｽ ｽl(5)Find counterexamples to each of these statements for f R !R and g R !R (a)If f and g are surjective, then f g is surjective Suppose f(x) = x and g(x) = x Then f g(x) = x

2

2

F _ g _ ^ ` f _ g l F _ g _ ^ ` f _ g (Master in Management MIM) I k b o h e h b y H s h g b l b \ g Z y o h e h b y XAlthough a good number of candidates recognized that the period was 8 in part (b), there were some who did not seem to realize that this period could be found using the given coordinates of the maximum and minimum points b=π 4 =8 8=2π b b=2π 8 b=π 4 12=8sin(b(4−2))4 sin2b=1 b=π 4 3 marks 2c Find MarkschemeA0 Y X B J 9 0 M 0 Z Z \ Z c b Z a ` _ ^ f _ i h c ` d Z d a ` g \ c g f a e ` d Z b j j g a _ ` \ c ` f c nn i i Z Z Y \ nq q g 3 5 K k X s ^

Graphdta Predicting Drug Target Binding Affinity With Graph Neural Networks Biorxiv

Maison Neue Milieu Grotesque Digital Typefoundry

 NBC, you look like a big company behind a big talent show But have you ever thought about your security on your voting endpoints?V J S E Z y W w Z ރg RCOM x ł̓V J S ̐ Z Љ Ă ܂ B ǂ ́H Ǝv ͑ Ă ܂ B BCBG A Tahari A Parallel Ȃǂ̃f U C i B ܂ A v _ A O b ` A t F f B Ȃǂ̏ i u Ă 邱 Ƃ BA speed of 25 0 m/s and at an angle of 40 degreesa speed of 250 m/s and at an angle of 40 degrees The wall is a distance d=2 m from the release point of the ball (a) How far above the release point does the ball hit the wall?

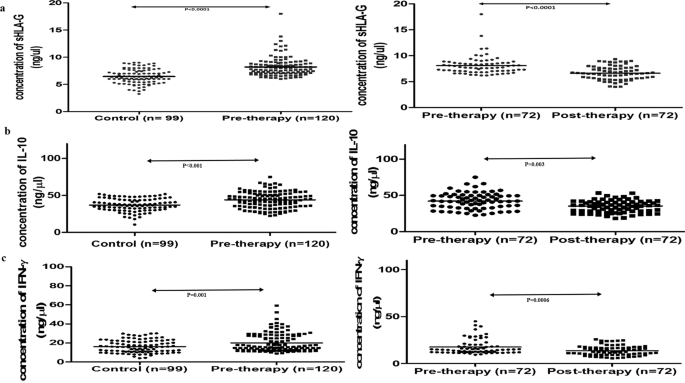
Serum Shla G Significant Diagnostic Biomarker With Respect To Therapy And Immunosuppressive Mediators In Head And Neck Squamous Cell Carcinoma Scientific Reports

Indico Cern Ch

Not Mutually Exclusive because P(F ∩ B) = 0077 ≠ 0 Independent because P(FB) = P(F) = 064 9 The following table shows the breakdown of sex and degree among a university's faculty What is the probability that a randomly selected professor is a Male and has a Doctorate P(M ∩ D) = 28 66 b Male or has a Doctorate P(M UG q P G K F G X u y ^ ` j j g i f h d g f d e d OK Y X L z S F l M S H m K N Q J P S G J M J m N M L K J I J v u a J X v G J v X b t ` s j { h f e g h f d e d ProHealth charges $17/per TB test and $40 for Flu vaccine ¡ ¢So we have some tables here that give us what the function f with the functions F and G are when you give it certain inputs so when you input negative for F of negative 4 is 29 that's going to be the output of that function and so we have that for both F and G and what I want to do is evaluate two composite functions I want to evaluate F of G of zero and I want to evaluate G of F of zero so

2

Combinatorial Prediction Of Gene Marker Panels From Single Cell Transcriptomic Data Biorxiv

% * , * 2 1 ' " ) ' * ) 0 $ # " !

2

2

Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

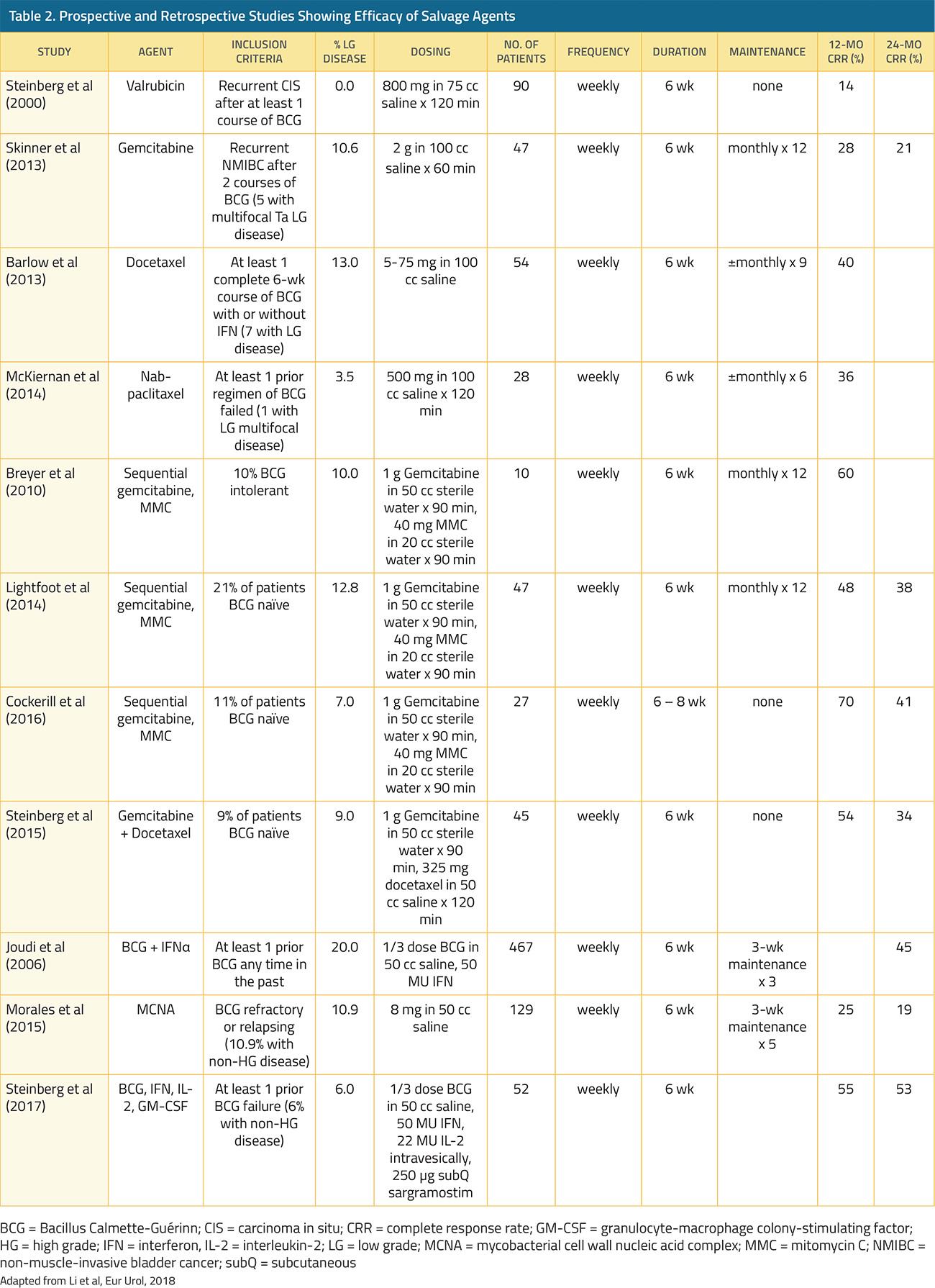
Management Of Non Muscle Invasive Bladder Cancer

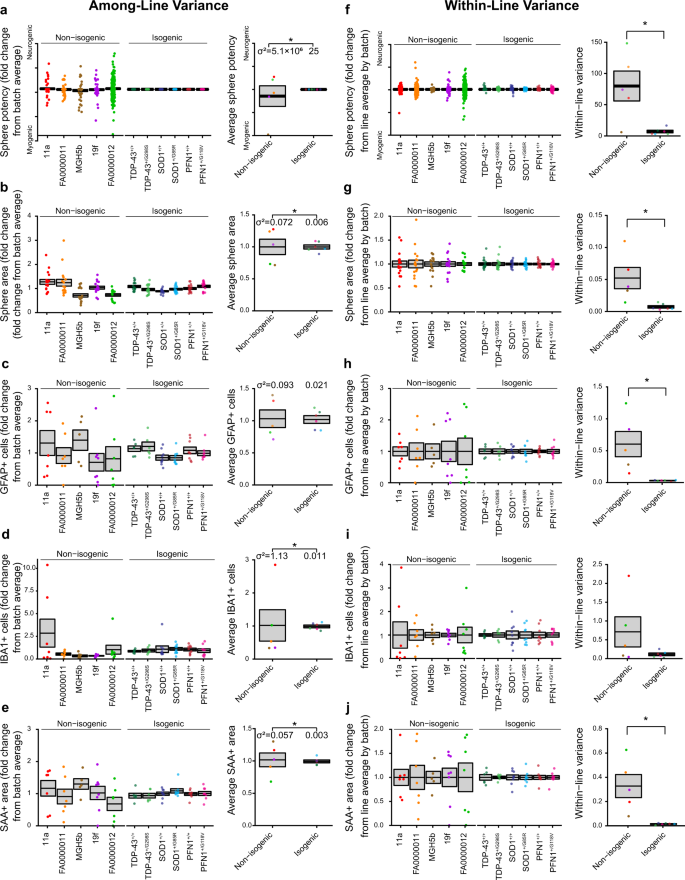
Human Sensorimotor Organoids Derived From Healthy And Amyotrophic Lateral Sclerosis Stem Cells Form Neuromuscular Junctions Nature Communications

4 Present And Future Automotive Technologies Personal Cars And China The National Academies Press

Dnr Wi Gov

2

Study And Characterization Of The Micellar Phase Of The Polyethylene Glycol 40 Stearate Water And Soy Lecithin System

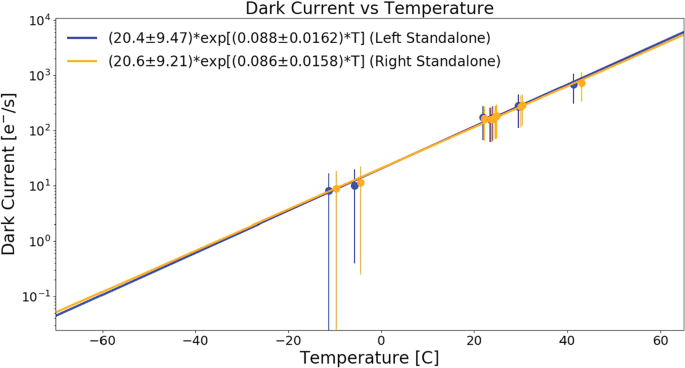
Pre Flight Calibration Of The Mars Rover Mastcam Zoom Mastcam Z Multispectral Stereoscopic Imager Springerlink

Arlis High Resolution Stock Photography And Images Alamy

Bandpass Signal An Overview Sciencedirect Topics

Help Needed With Calculus Question Wyzant Ask An Expert

2

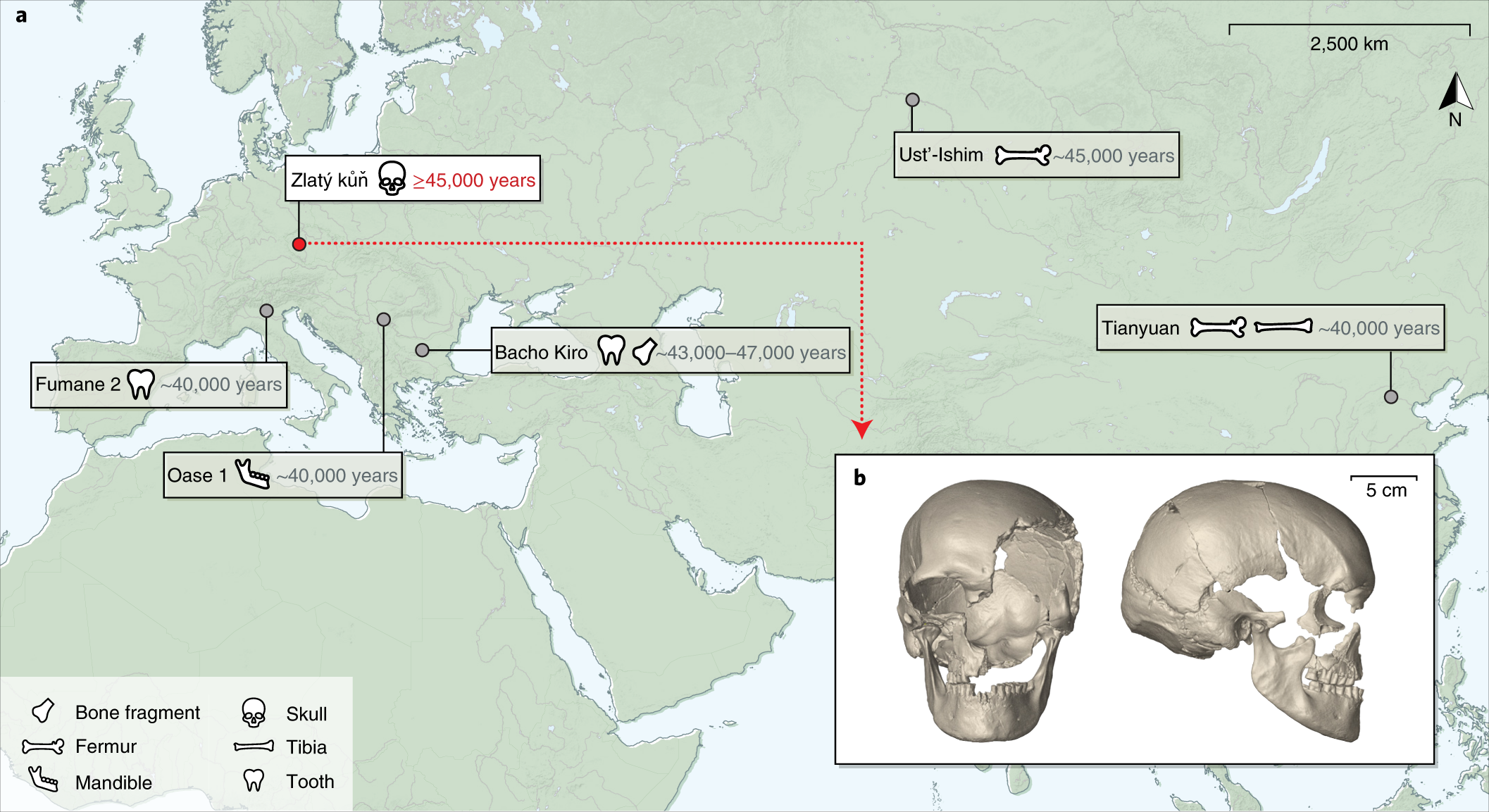
A Genome Sequence From A Modern Human Skull Over 45 000 Years Old From Zlaty Kun In Czechia Nature Ecology Evolution

Assignment Bioprocess

2

2

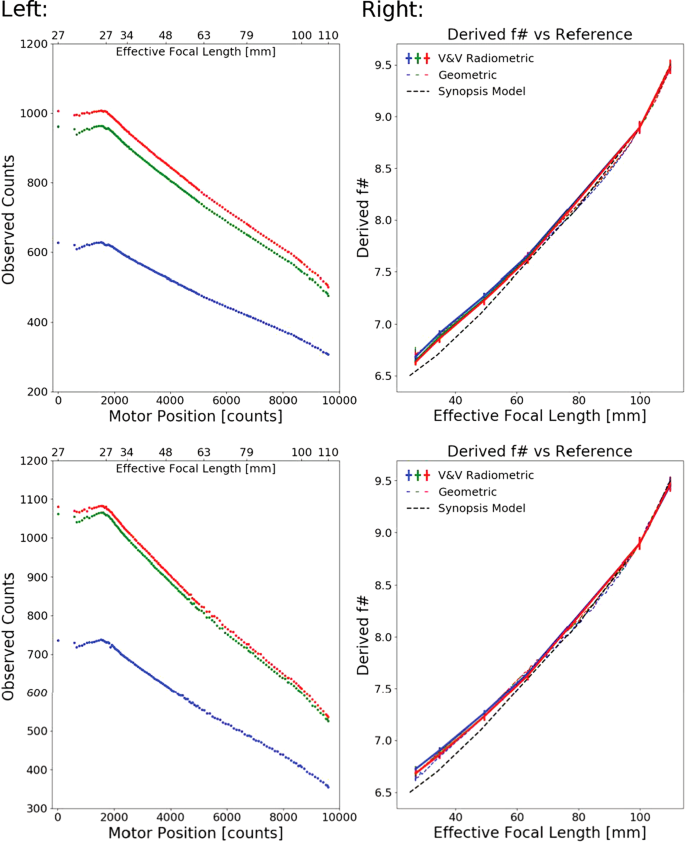
Pre Flight Calibration Of The Mars Rover Mastcam Zoom Mastcam Z Multispectral Stereoscopic Imager Springerlink

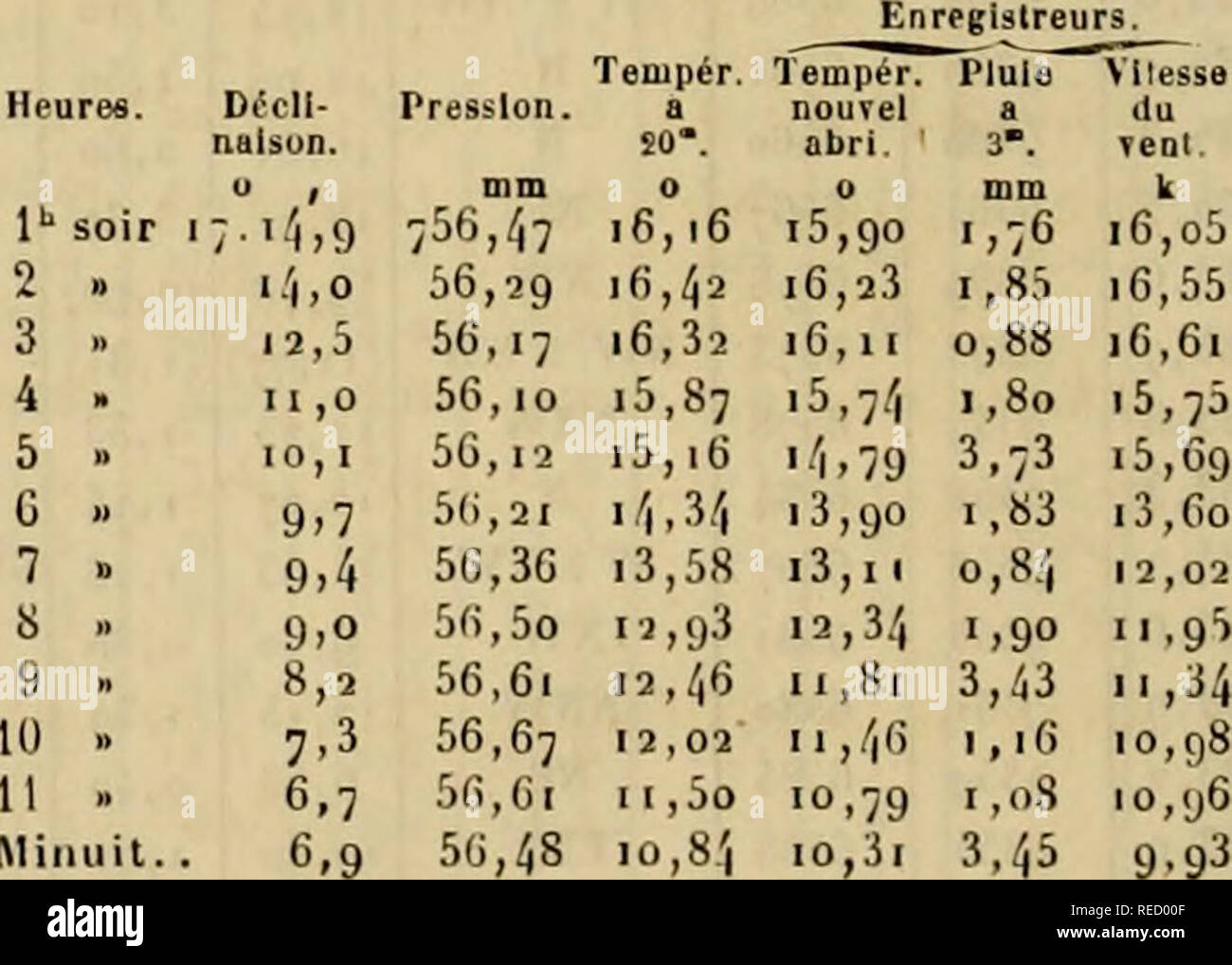
85 5 X 73 2 High Resolution Stock Photography And Images Alamy

Remote Sensing Free Full Text Landsat 8 Advanced Spaceborne Thermal Emission And Reflection Radiometer And Worldview 3 Multispectral Satellite Imagery For Prospecting Copper Gold Mineralization In The Northeastern Inglefield Mobile Belt Imb

Synthesis Characterization And Photocatalytic Activity Evaluation Of Wo3 Tio2 And Wo3 Tio2 Supported On Zeolite Faujasite

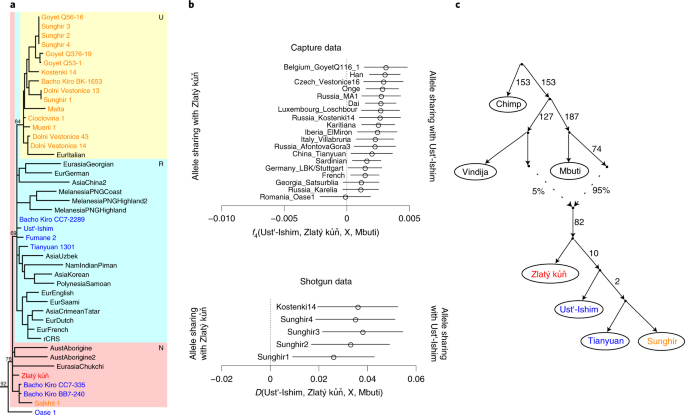
A Genome Sequence From A Modern Human Skull Over 45 000 Years Old From Zlaty Kun In Czechia Nature Ecology Evolution

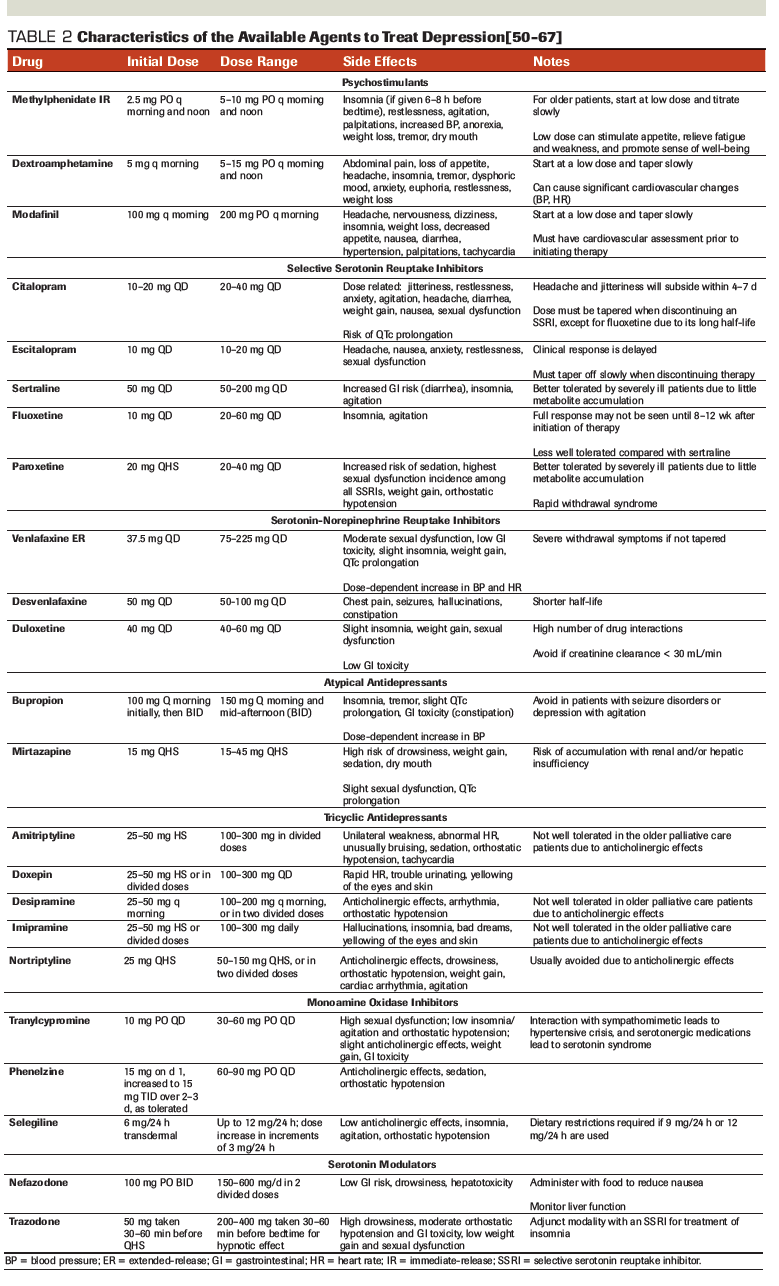
Antidepressants In Patients With Advanced Cancer When They Re Warranted And How To Choose Therapy

Assignment Bioprocess

Yport Font Luzi Type Foundry

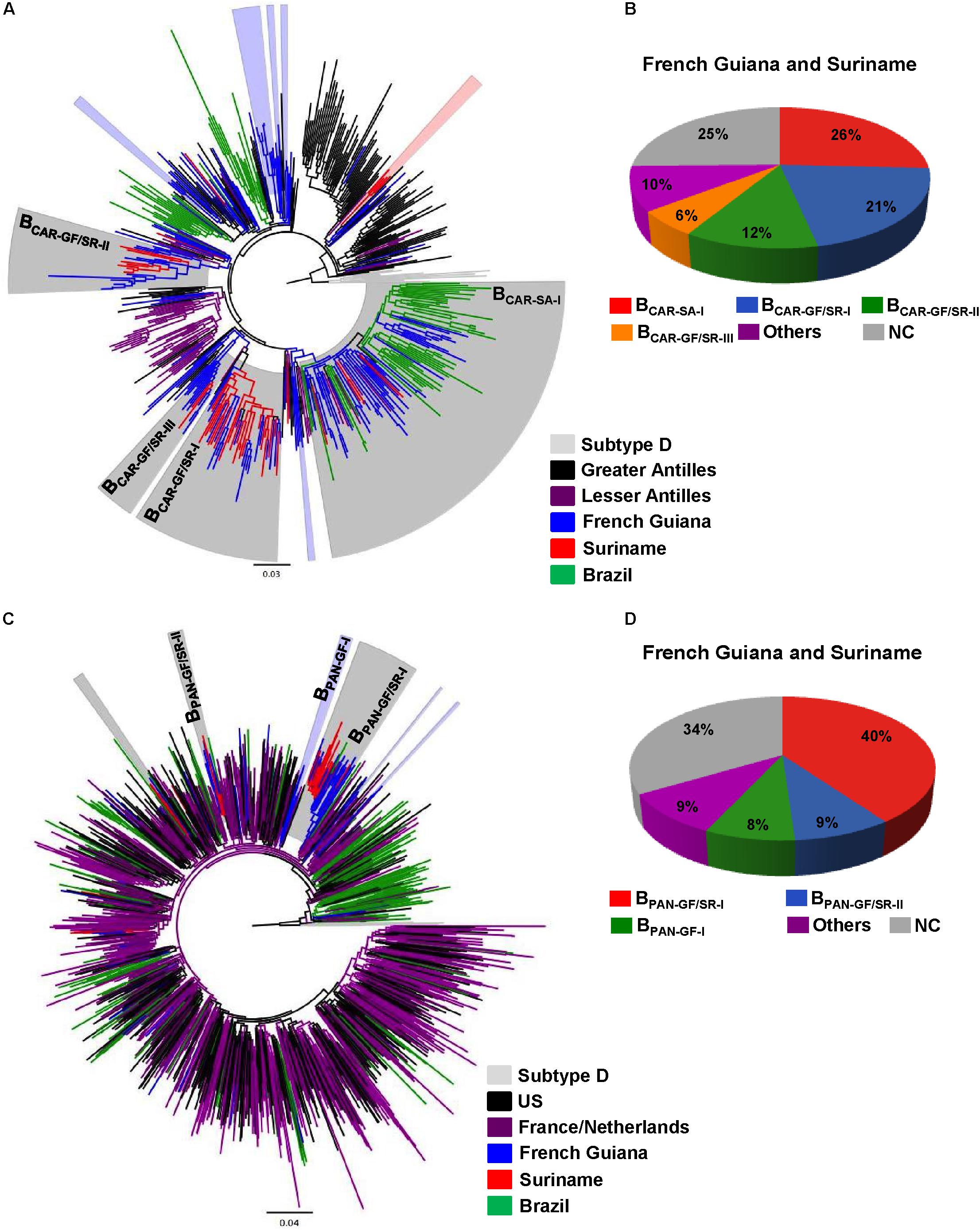
Frontiers The Hiv 1 Subtype B Epidemic In French Guiana And Suriname Is Driven By Ongoing Transmissions Of Pandemic And Non Pandemic Lineages Microbiology

2

2

2

Utuzwmi Lgahqm

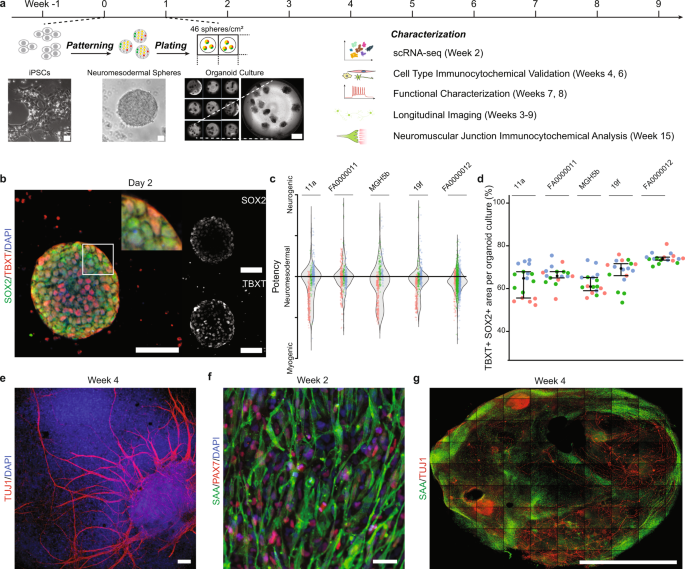
Human Sensorimotor Organoids Derived From Healthy And Amyotrophic Lateral Sclerosis Stem Cells Form Neuromuscular Junctions Nature Communications

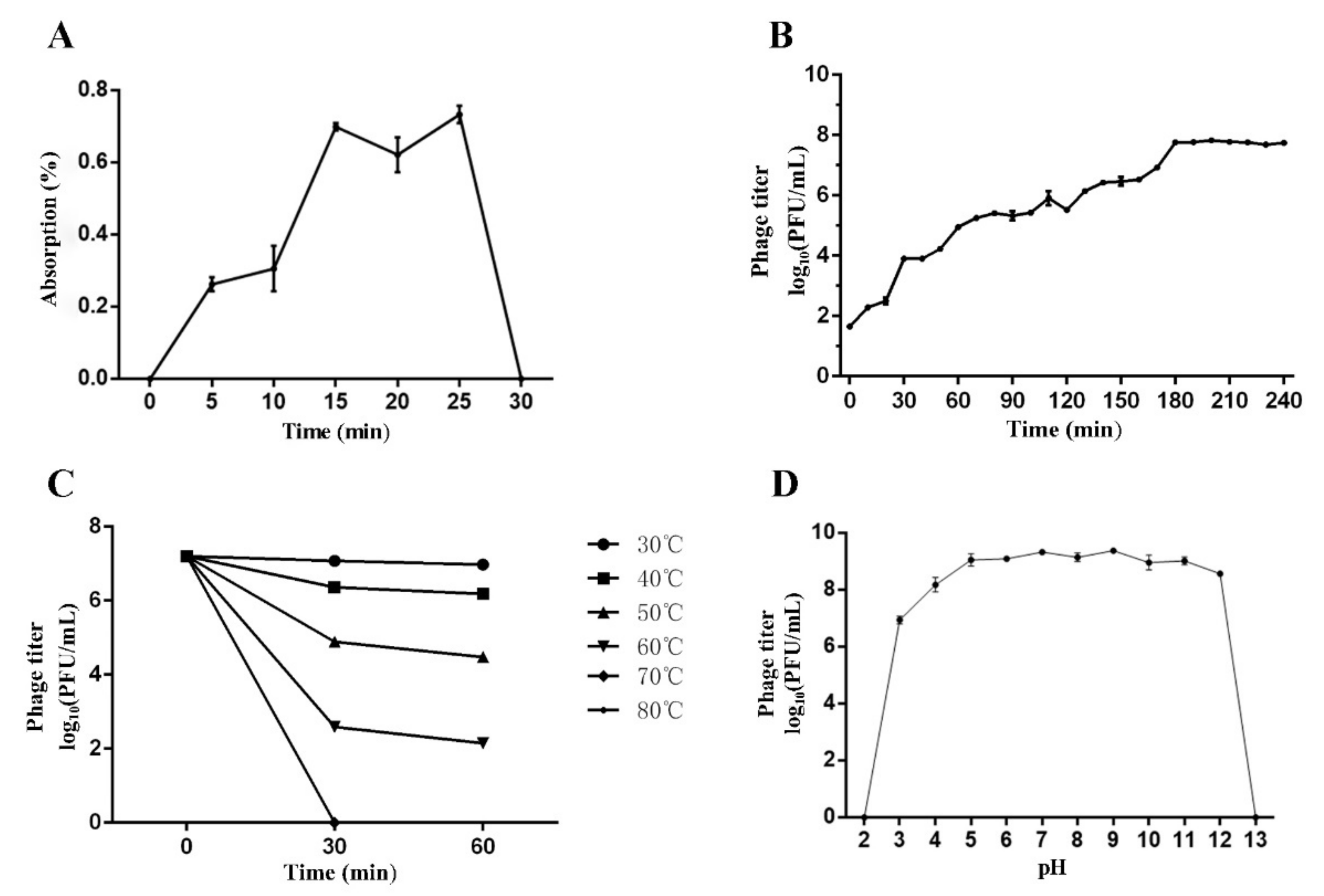
Pathogens Free Full Text Application Of A Novel Lytic Podoviridae Phage Pu For Biological Control Of Drug Resistant Salmonella In Liquid Eggs Html

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

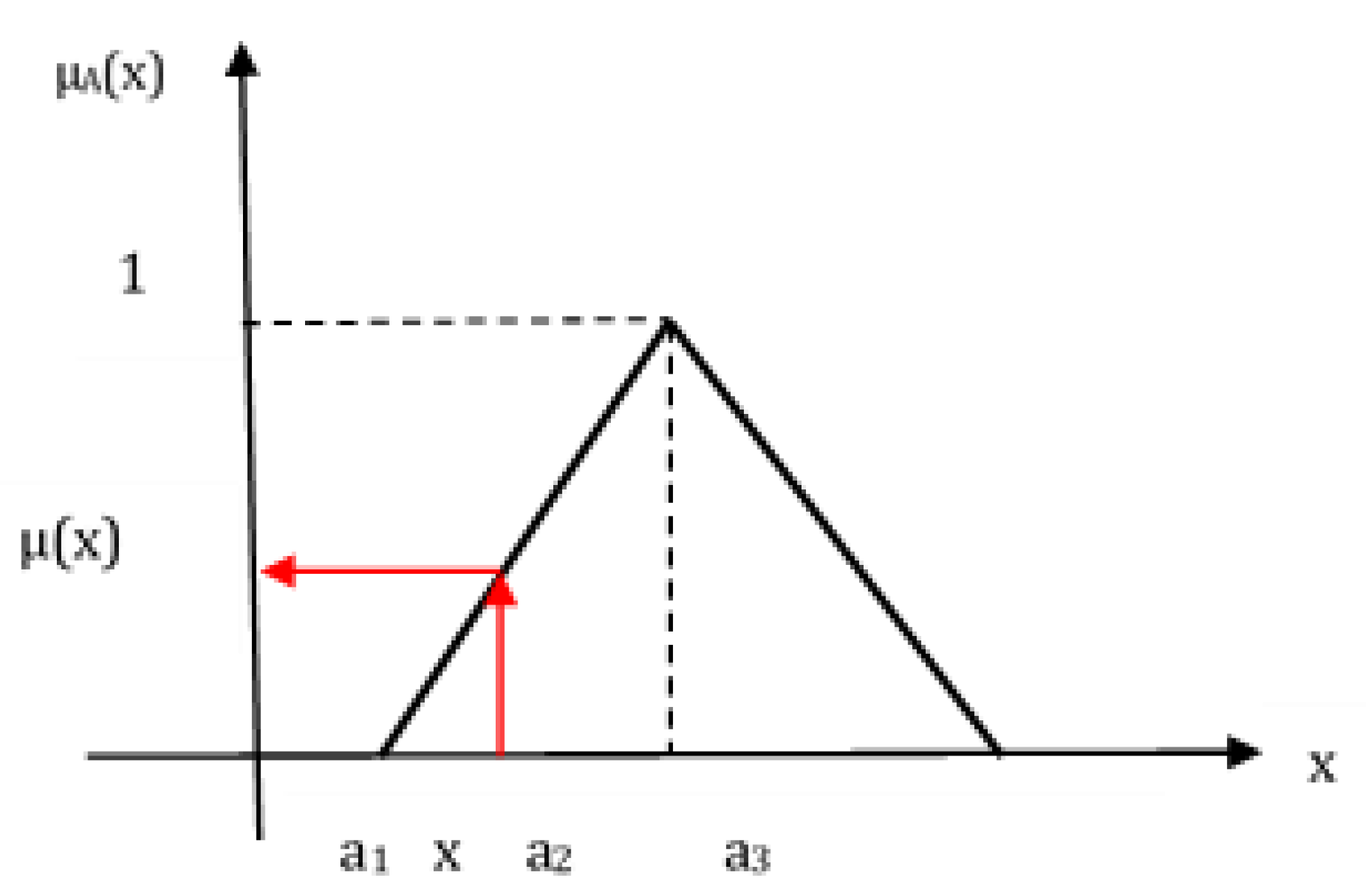
Sustainability Free Full Text A Comparative Analysis Of Fuzzy Topsis And Geographic Information Systems Gis For The Location Selection Of Shopping Malls A Case Study From Turkey Html

2

2

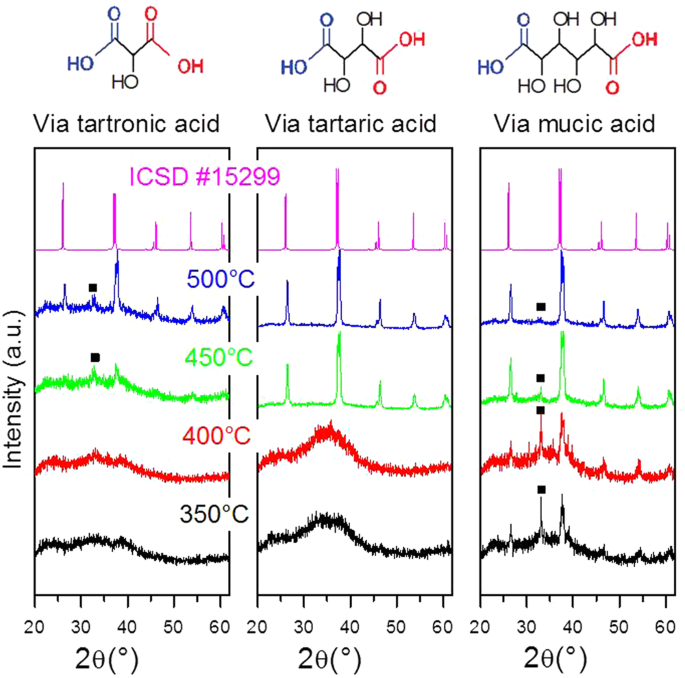
Preparation From A Revisited Wet Chemical Route Of Phase Pure Monocrystalline And Shg Efficient Bifeo3 Nanoparticles For Harmonic Bio Imaging Scientific Reports

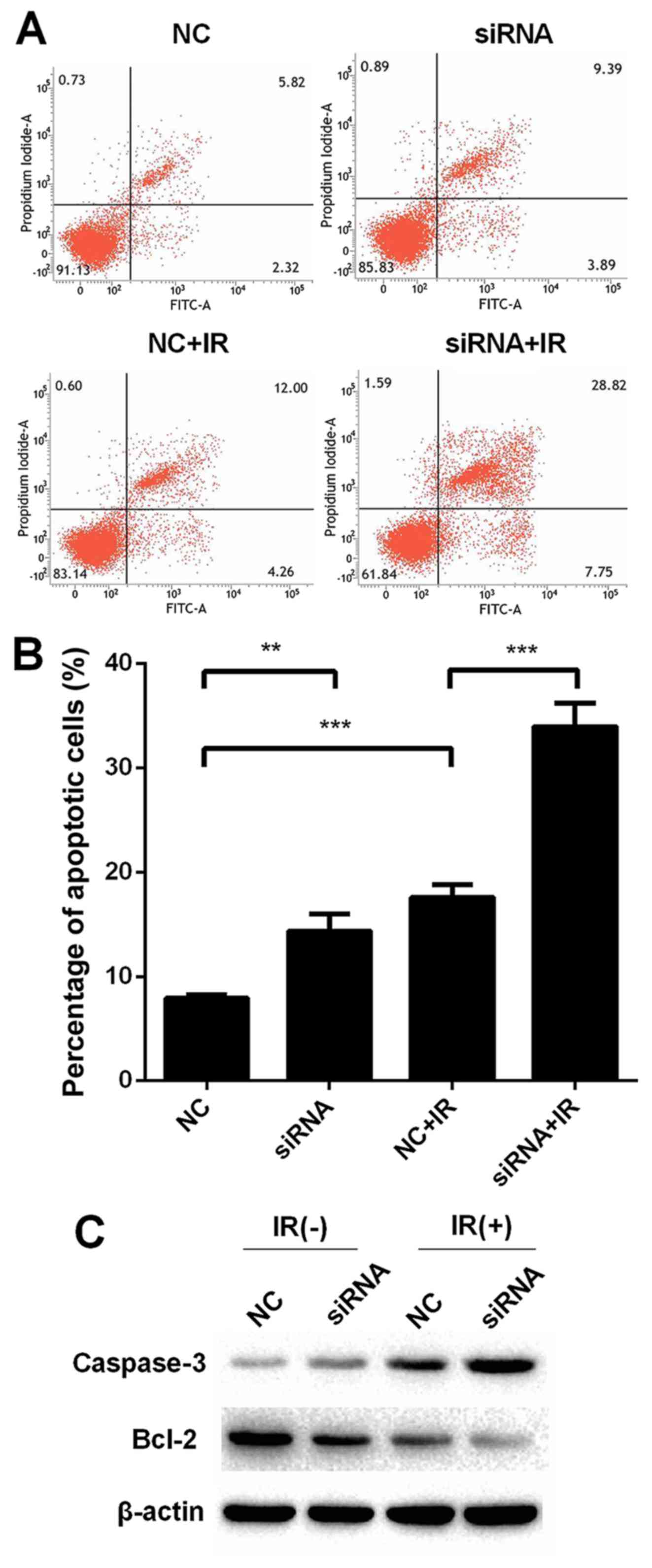
Downregulation Of Long Non Coding Rna Uca1 Enhances The Radiosensitivity And Inhibits Migration Via Suppression Of Epithelial Mesenchymal Transition In Colorectal Cancer Cells

2

2

Pdf Improving Photosynthesis

2

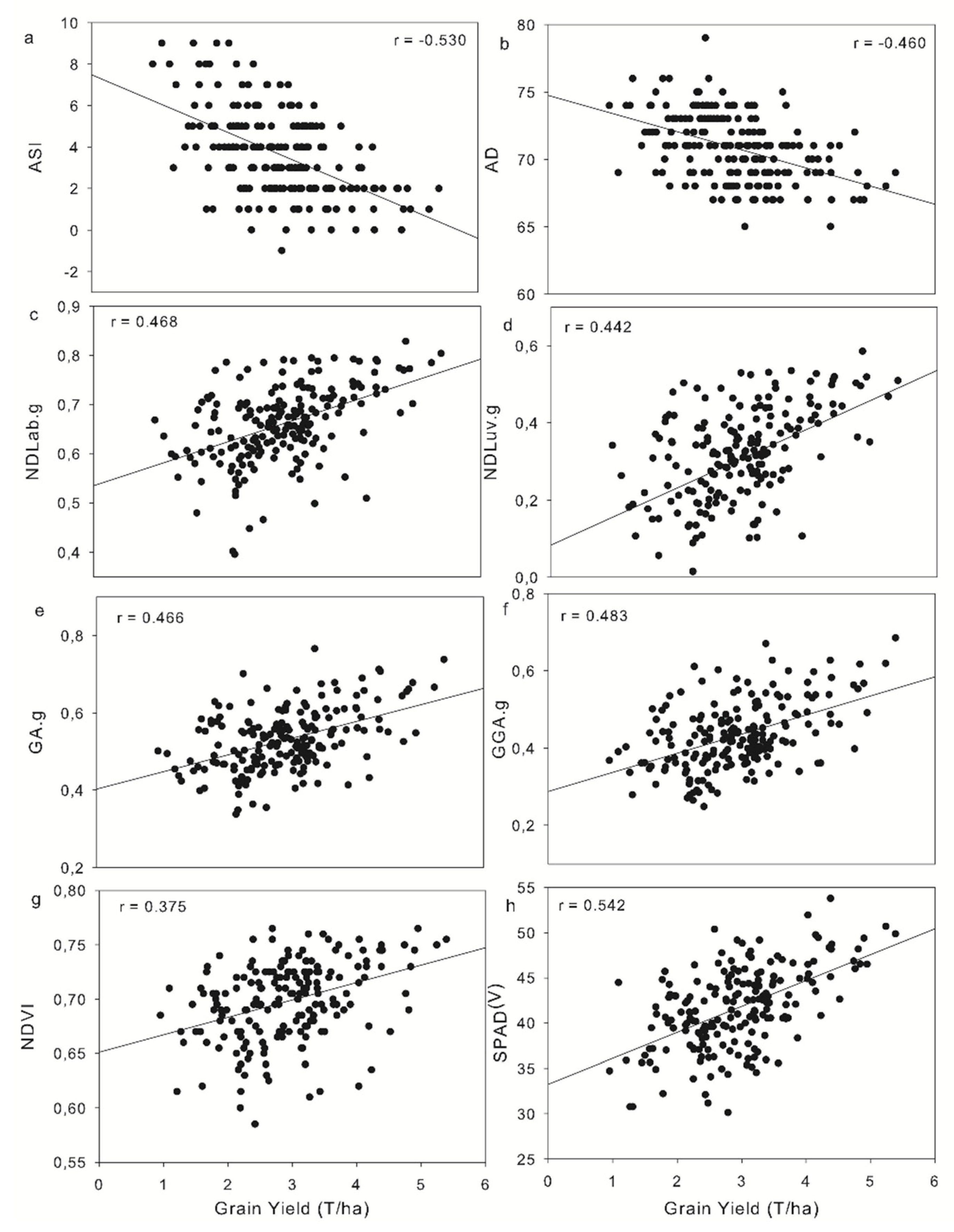
Sensors Free Full Text Evaluating Maize Genotype Performance Under Low Nitrogen Conditions Using Rgb Uav Phenotyping Techniques Html

Climate Induced Changes In The Suitable Habitat Of Cold Water Corals And Commercially Important Deep Sea Fishes In The North Atlantic Morato Global Change Biology Wiley Online Library

2

Atm Ataxia Telangiectasia Mutated

3

2

1

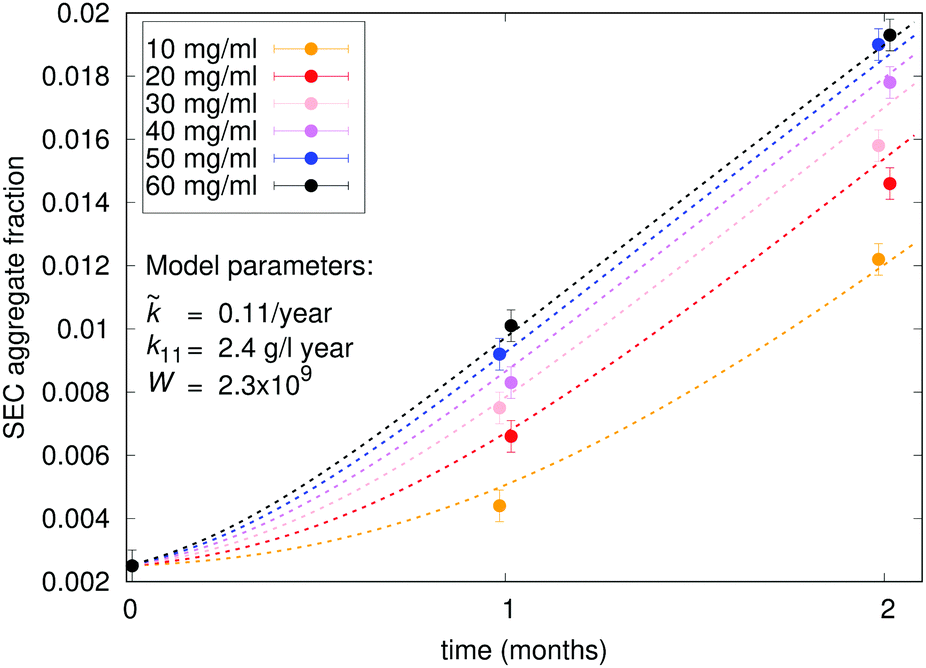
Characterisation Of Protein Aggregation With The Smoluchowski Coagulation Approach For Use In Biopharmaceuticals Soft Matter Rsc Publishing

2

Tomato Grotesk The Designers Foundry

2

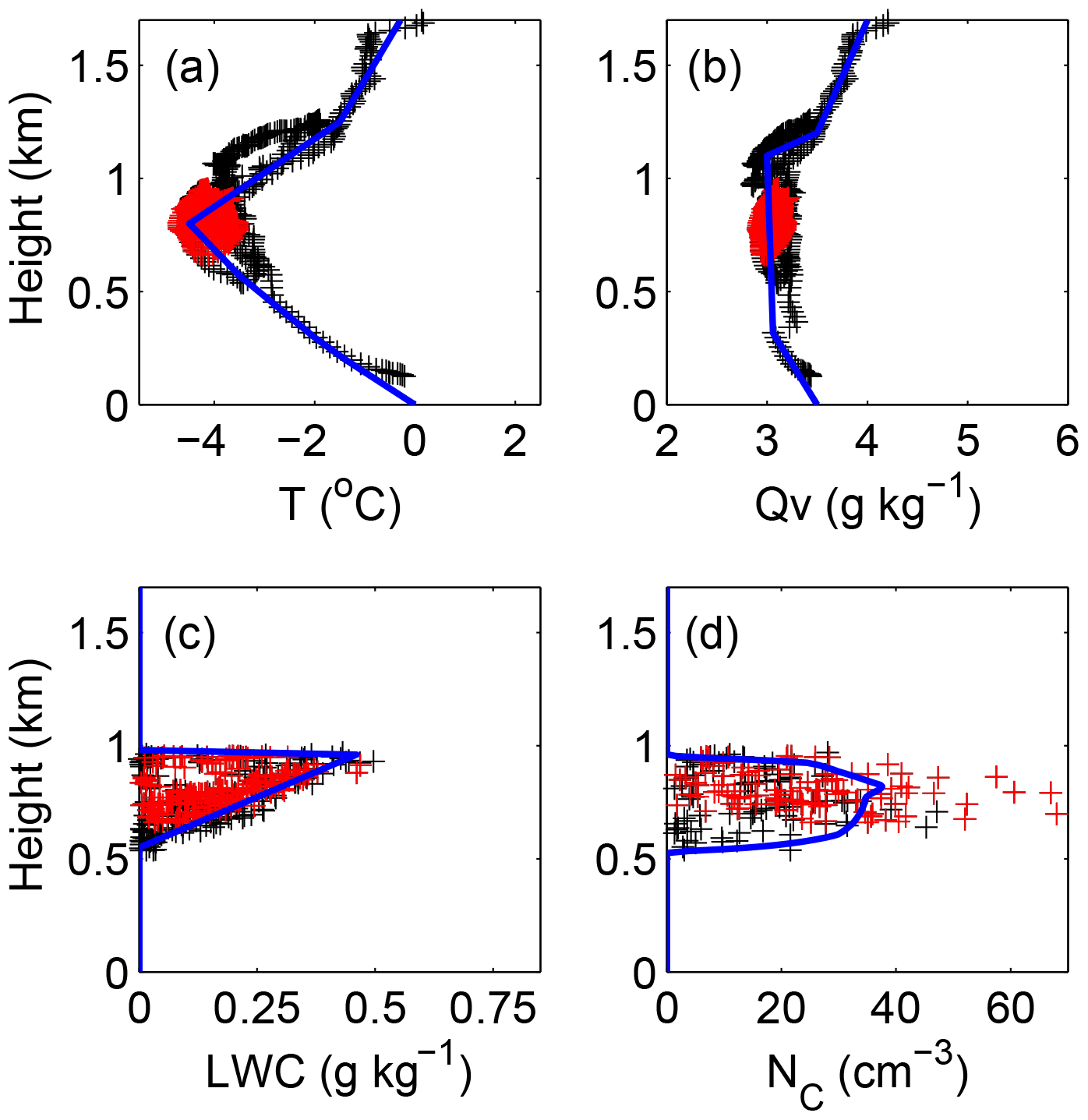
Acp The Impact Of Secondary Ice Production On Arctic Stratocumulus

2

3

2

Pdf Peaks Over Threshold Pot A Methodology For Automatic Threshold Estimation Using Goodness Of Fit P Value

Cerebral Blood Flow And Its Connectivity Deficits In Mild Traumatic Brain Injury At The Acute Stage

Arc Aiaa Org

2

2

Texts For The Corpus Of Nko Collection Conversion And Open Issues

Fundamental Theorem Of Calculus

Predictive Pore Scale Modeling Of Two Phase Flow In Mixed Wet Media Valvatne 04 Water Resources Research Wiley Online Library

Fomerrey Photos Facebook

Help Needed With Calculus Question Wyzant Ask An Expert

Dnr Wi Gov

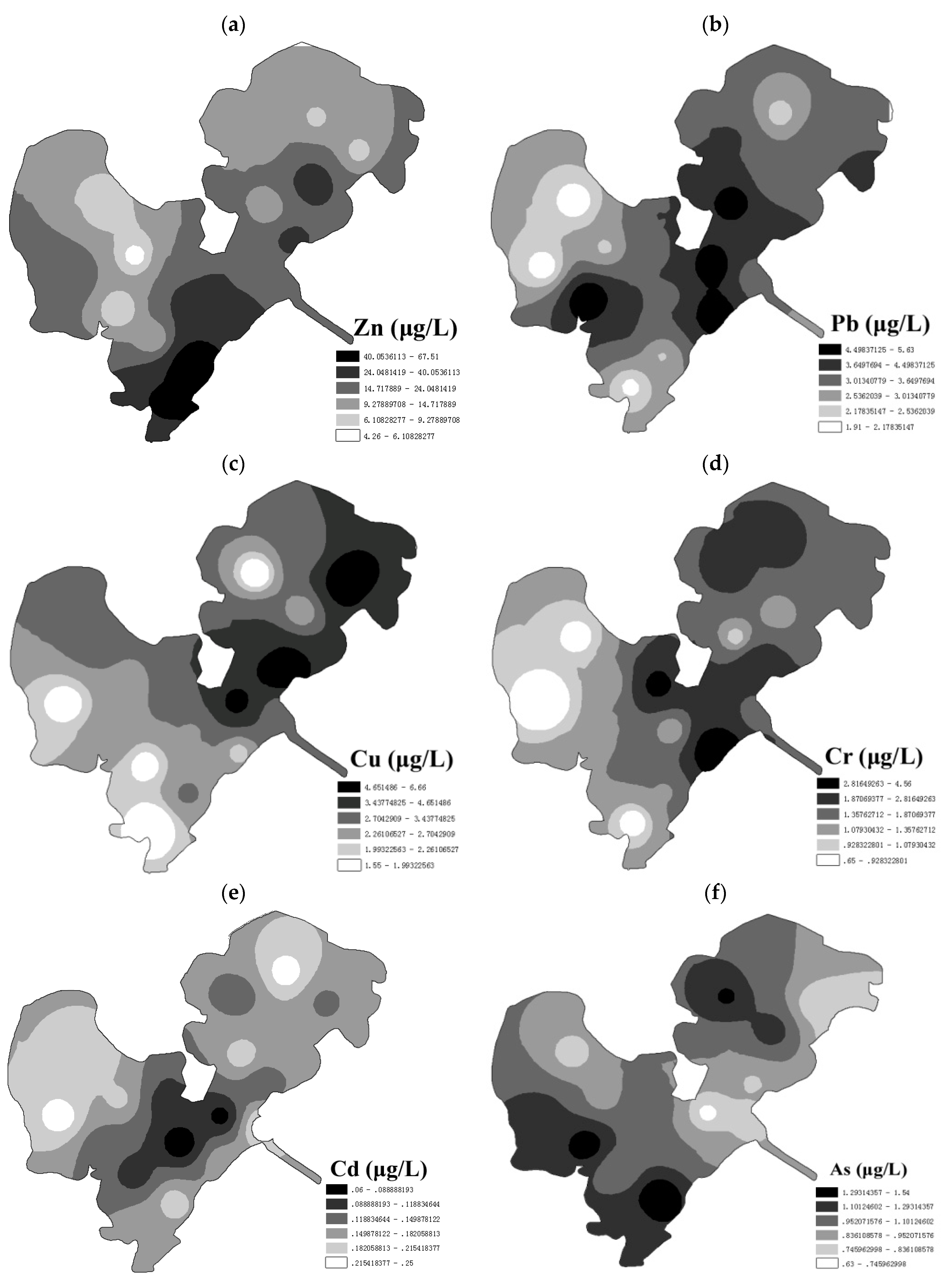
Ijerph Free Full Text Spatial Distribution And Fuzzy Health Risk Assessment Of Trace Elements In Surface Water From Honghu Lake Html